Question
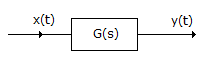
a.
A sin (ωt + φ) where φ = tan¯¹ |G(jω)|
b.
|G(jω)| A sin [ωt + ∠G(jω)]
c.
|G(jω)| A sin [2ωt + ∠G(jω)]
d.
A G(jω) sin [ωt + ∠G(jω)]
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. In the given figure the input is x(t) = A sin ωt. The steady state output y(t) =
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. In the given figure x6 =
View solution
Q. For the given figure, C(s)/R(s) =
View solution
Q. For the control system in the given figure, the value of K for critical damping is
View solution
Q. For the system in the given figure, C(s)/R(s) =
View solution
Q. In the given figure, if R = XC, voltage gain is
View solution
Q. For the circuit in the given figure, V2(s)/V1(s) =
View solution
Q. The system in the given figure, has
View solution
Q. The given figure shows a pole zero diagram. The transfer function G(j1) is
View solution
Q. For very low frequencies, v0/vi in the given figure equals
View solution
Q. For the system of the given figure the transfer function is
View solution
Q. The first column of a Routh array is given below. How many roots of the corresponding characteristic equation are in left half s-plane?
View solution
Q. For the given figure, time constant RC = t. Then Vo(s)/Vi(s) =
View solution
Q. In the given figure, C(s) =
View solution
Q. For G(jω) =
View solution
Q. The transient response of a second order system is given by following equation. For 5% criterion the settling time is
View solution
Q. For the system in the given figure, the transfer function C(s)/R(s) is
View solution
Q. For the system in the given figure, the characteristic equation is
View solution
Q. In the given figure the transfer function C(s)/N(s) =
View solution
Q. The following transfer function can be for
View solution
Q. The system of the given figure
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








