Question
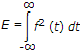
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The energy associated with a function f(t) is given below. In terms of Fourier transform, E =
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The distance of a synchronous satellite from Earth's surface is __________ km.
View solution
Q. A function having frequency f is to be sampled. The sampling time T should be
View solution
Q. Inverse Fourier transform of sgn (ω) is
View solution
Q. If I (s) = 5(s+250)/s(s+100) , the final value of i(t) is
View solution
Q. The signal defined by the equations f(t) = 0 for t < 0, f(t) = E for 0 ≤ t ≤ a and f(t) = 0 for t > a is
View solution
Q. Inverse Laplace transform of 2s+5 / (s²+5s+6) is
View solution
Q. Two function g1(t) and g2(t) with correlation of 6 has average power of 4 and 5 respectively. The power of g1(t) + g2(t) is
View solution
Q. A box has 4 white and 3 red balls. Two balls are taken out in succession. What is the probability that both are white?
View solution
Q. Z transform is a non-linear operation.
View solution
Q. Which one most appropriate dynamic system?
View solution
Q. An energy signal has G(f) = 10. Its energy density spectrum is
View solution
Q. In an ac circuit the fundamental component of current wave lags the corresponding voltage wave by 20°. The third harmonic component of current wave lags the corresponding voltage by an angle.
View solution
Q. A signal g(t) = A then g(t) is a
View solution
Q. The Fourier series of an odd periodic function contains
View solution
Q. An impulse function consist of
View solution
Q. As per time displacement theorem in Laplace transformation, displacement in the time domain by T becomes
View solution
Q. If transfer function of a system is H(z) = 6 + z¯¹ + z¯², then system is
View solution
Q. Which one is a linear system?
View solution
Q. Which one is a causal system?
View solution
Q. Double integration of a unit step function would lead to
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!