Question
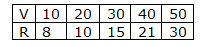
a.
6.7 + 0.0092 V²
b.
3 + 0.001 V²
c.
3.2 + 0.0012 V²
d.
5.2 + 0.006 V²
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The data of speed of train V and resistance to motion R is given below. The law R = a + bV² is of the form
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. If H(z) is given by following equation, then system is
View solution
Q. If F(s) = 10 / s²+4s+4, f(t) =
View solution
Q. Consider z transform of a signal as given below, then the response will be
View solution
Q. The eigen values of the following matrix are
View solution
Q. The initial value theorem is
View solution
Q. Consider following two statements:
View solution
Q. The exponential form of Fourier series is
View solution
Q. The unit step response of a system starting from rest is given by c(t) = 1 - e^(-2t) for t ≥ 0. The transfer function of the system is
View solution
Q. Check the following system for causality
View solution
Q. Paley Wiener criterion for designing of filter is
View solution
Q. The Laplace transform of cos ωt is
View solution
Q. The response of a linea, time invariant discrete time system to a unit step input ∪(n) is the unit impulse δ(n). The system response to a ramp input n ∪(n) would be
View solution
Q. The impulse response h[n] of a linear time invariant system is given as below. If the input to the above system is the sequence e^(jπn/4), then the output is
View solution
Q. In the periodic train of rectangular pulses F₀ = (V₀/T)d
View solution
Q. Z transform of [(Xk±k₀)] =
View solution
Q. If f(t) ↔ F(jω), and f(t) is real, then
View solution
Q. Initial value theroem for sequence x[n] is
View solution
Q. The energy E associated with time function f(t) is
View solution
Q. If F[jω] is Fourier transform of f(t), then Fourier transform of f(- t) =
View solution
Q. The solution of state equations using Laplace transform is
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!