Question
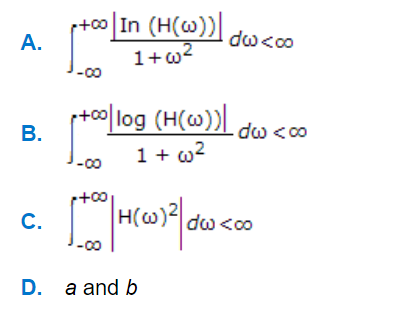
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. Paley Wiener criterion for designing of filter is
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The Laplace transform of cos ωt is
View solution
Q. The response of a linea, time invariant discrete time system to a unit step input ∪(n) is the unit impulse δ(n). The system response to a ramp input n ∪(n) would be
View solution
Q. The impulse response h[n] of a linear time invariant system is given as below. If the input to the above system is the sequence e^(jπn/4), then the output is
View solution
Q. In the periodic train of rectangular pulses F₀ = (V₀/T)d
View solution
Q. Z transform of [(Xk±k₀)] =
View solution
Q. If f(t) ↔ F(jω), and f(t) is real, then
View solution
Q. Initial value theroem for sequence x[n] is
View solution
Q. The energy E associated with time function f(t) is
View solution
Q. If F[jω] is Fourier transform of f(t), then Fourier transform of f(- t) =
View solution
Q. The solution of state equations using Laplace transform is
View solution
Q. Consider the following statements:
View solution
Q. e^(At) can be expanded as
View solution
Q. Consider the following and answer accordingly:
View solution
Q. The function in the given figure can be written as
View solution
Q. Consider the following as regards probability distribution function f(x). which of these are correct?
View solution
Q. Inverse Fourier transform of ∪(ω) is
View solution
Q. The triangular wave of the given figure can be written as v(t) = u(t) - tu(t) + (t - 1) u(t - 1)
View solution
Q. The function shown in the figure
View solution
Q. Consider the following statements :
View solution
Q. If Fn represents Fourier series coefficient of f(t), then Fourier series coefficient of f(t + t) =
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








