Question
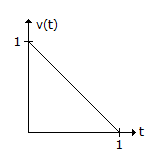
a.
True
b.
False
c.
May be True or False
d.
Can't Say
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The triangular wave of the given figure can be written as v(t) = u(t) - tu(t) + (t - 1) u(t - 1)
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The function shown in the figure
View solution
Q. Consider the following statements :
View solution
Q. If Fn represents Fourier series coefficient of f(t), then Fourier series coefficient of f(t + t) =
View solution
Q. Fourier transform of unit step function is
View solution
Q. Auto correlation R(t) of a function v(t) is defined as
View solution
Q. Parseval's theorem for energy tells that
View solution
Q. For Binomial Distribution
View solution
Q. If f1(t) ↔ F1 (jω) and f2(t) ↔ F2(jω), then f1(t)↔ f2(t)
View solution
Q. A wave f(t) has half wave symmetry and time period equal to T. Then
View solution
Q. The two inputs to an analogue multiplier are x(t) and y(t) with fourier transforms X(f) and Y(f) respectively. The output Z(t) will have a transform Z(f) given by
View solution
Q. If v(t) = 0 for t < 0 and v(t) = e^(-at) for t ≥ 0, V(jω) =
View solution
Q. Consider the following equation.
View solution
Q. Which of the following can be impulse response of a casual system?
View solution
Q. The Laplace transform of sin ∝ t is
View solution
Q. Fourier transform of the unit step function (i.e., u(t) = 1 for t ≥ 0 and u(t) = 0 for t < 0) is
View solution
Q. The dirac delta function δ(t) is defined as
View solution
Q. Laplace transforn of sin (ωt + a) is
View solution
Q. If x^k = 2^k for k ≤ 0 and xk = 0 for k ≥ 0, Z transform of the sequence x is
View solution
Q. Final value theroem is for sequence x[n] is
View solution
Q. The Laplace transform of (tⁿ-1) where n is integer is
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!