Question
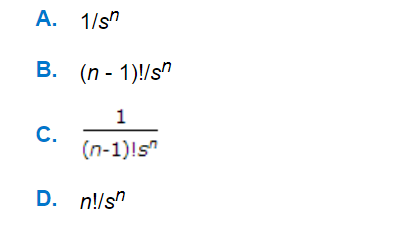
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The Laplace transform of (tⁿ-1) where n is integer is
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The data about p the pull required to lift a weight wby a pulley block is given below. The linear law p = a + bw is
View solution
Q. Average power for following signal is
View solution
Q. Which is the Laplace transform of x(t) = -e^(2t) ∪(t) ⊕ t ∪(t)?
View solution
Q. For a signal x(t) the F.T. is X(f). Then inverse F.T of X(3f + 2) is given by
View solution
Q. An experiment is repeated N times. One event A occurs Nᴀ times. Then
View solution
Q. If f(t) is an even function, F(jω) =
View solution
Q. If Laplace transform of f(t) is F(s), then £[tf(t)] =
View solution
Q. The minimum sampling frequency in sample/sec. required to reconstruct the following signal from its samples without distortion would be
View solution
Q. The function shown in the given Figure can be written as
View solution
Q. In a network V(s) = Z(s) I(s) where V(s), Z(s) and I(s) are Laplace transforms of v(t), z(t) and i(t). The voltage v(t) is
View solution
Q. As per normal distribution the probability of an error between limits a and b is
View solution
Q. If F(jω) is the Fourier transform of f(t) then f(t) =
View solution
Q. The Laplace transform of sin ωt is
View solution
Q. If f(t) is an even function
View solution
Q. The waveform shown in the given Figure can be written as
View solution
Q. If a function f(t) is Laplace transformable, then
View solution
Q. In the given figure shows a periodic triangular wave. The Fourier series will have
View solution
Q. If x^k is one sided to the right
View solution
Q. A discrete LTI system is non-casual if its impulse response is
View solution
Q. If f(t) is an odd function
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!