Question
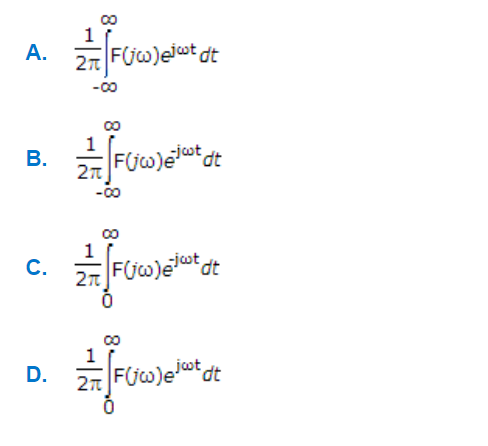
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. If F(jω) is the Fourier transform of f(t) then f(t) =
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The Laplace transform of sin ωt is
View solution
Q. If f(t) is an even function
View solution
Q. The waveform shown in the given Figure can be written as
View solution
Q. If a function f(t) is Laplace transformable, then
View solution
Q. In the given figure shows a periodic triangular wave. The Fourier series will have
View solution
Q. If x^k is one sided to the right
View solution
Q. A discrete LTI system is non-casual if its impulse response is
View solution
Q. If f(t) is an odd function
View solution
Q. The inverse z-transform of X(z) is
View solution
Q. The impulse response of the DT - LTI system is given below.
Check whether the system is
1. Stable
2. Casual
3.Dynamic
View solution
Q. For the single rectangular pulse of the given figure:
F(jω) = [Ad sin (ωd/2)]/(ωd/2).
View solution
Q. If p is the probability of success and q is the probability of failure, then the probability that there are r successes in n trails is
View solution
Q. A signal m(t) with bandwidth 500 Hz is first multiplied by a signal g(t) where g(t) ids given by below equation. The resulting signal is then passed through on ideal low pass filter with bandwidth 1 kHz. The output of the low pass filter would me
View solution
Q. The Z.T. of sequence x[n] = aⁿ ∪ [n] is
View solution
Q. The unit step response of a system is (1 - e^(at)) u(t). Then its impulse response is
View solution
Q. The inverse Laplace transform of 1/(s - a)² is
View solution
Q. Which one of the following digital filters does have a linear phase response?
View solution
Q. cos(nω1t) =
View solution
Q. Fourier transform of e^(-a|t|) is
View solution
Q. Assertion (A): The wave shown in the given figure does not contain the dc component and even harmonics.
Reason (R): If f(- t) = f(t) the wave has only cosine terms.
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








