Question
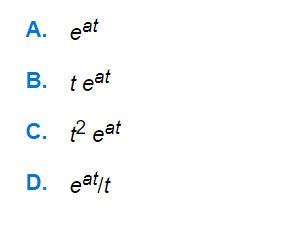
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The inverse Laplace transform of 1/(s - a)² is
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. Which one of the following digital filters does have a linear phase response?
View solution
Q. cos(nω1t) =
View solution
Q. Fourier transform of e^(-a|t|) is
View solution
Q. Assertion (A): The wave shown in the given figure does not contain the dc component and even harmonics.
Reason (R): If f(- t) = f(t) the wave has only cosine terms.
View solution
Q. If £ f(t) = F(jω), then
View solution
Q. If n is the number of observations and r is the residue, the standard deviation σ =
View solution
Q. Consider these tow statements and answer follow:
View solution
Q. Consider following statements:
View solution
Q. Consider below given statements:
View solution
Q. The z transform of fk = a^k is
View solution
Q. In the given figure f(t) is an even function.
View solution
Q. Which of the following is not true for impulse function δ(t)?
View solution
Q. In the given figure the phase angle of Fn is either 0 or Π.
View solution
Q. For the function f(t) = e^(-at), the Laplace transform is
View solution
Q. The Z inverse of the given Z transform is
View solution
Q. Consider the following two statements :
View solution
Q. Consider the following two statements :
View solution
Q. If x(z) is the Z transform of sequence xk, the z transform of sequence (kxk)is
View solution
Q. If Sn is the power associated with each frequency component and S(f) is the sum of all these powers, normalised power spectral density is
View solution
Q. For the signal in the given figure the Fourier transform is 2sinωΤ₁, then the Fourier transform of the signal in the given figure
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!