Question
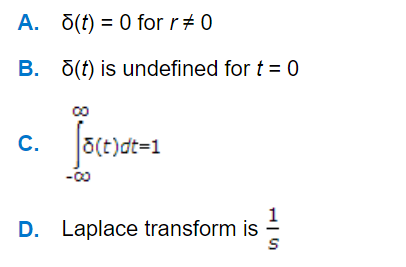
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. Which of the following is not true for impulse function δ(t)?
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. In the given figure the phase angle of Fn is either 0 or Π.
View solution
Q. For the function f(t) = e^(-at), the Laplace transform is
View solution
Q. The Z inverse of the given Z transform is
View solution
Q. Consider the following two statements :
View solution
Q. Consider the following two statements :
View solution
Q. If x(z) is the Z transform of sequence xk, the z transform of sequence (kxk)is
View solution
Q. If Sn is the power associated with each frequency component and S(f) is the sum of all these powers, normalised power spectral density is
View solution
Q. For the signal in the given figure the Fourier transform is 2sinωΤ₁, then the Fourier transform of the signal in the given figure
View solution
Q. Let x(t) ↔ X(jω) be F.T pair. The Fourier transform of the signal x(5t - 3) in terms of X(jω) is given as
View solution
Q. Assertion (A): The Fourier series of the wave shown in the figure does not contain even harmaonics.
Reason (R): If f(t) = - f(t ± T/2) the function is said to have half wave symmetry.
View solution
Q. The following table gives some time functions and the Laplace transforms. Of these correctly matched pairs are
View solution
Q. The given figure shows a square wave i(t). Then I(s) =
View solution
Q. If the region of convergence of x1(n) + x2(n) is 1/3 < |z| < 2/3, then the region of convergence of x1[n] - x2[n] includes
View solution
Q. If f(t) ↔ F(jω),
View solution
Q. If f(t) is an odd function, F(jω) =
View solution
Q. The energy associated with a function f(t) is given below. In terms of Fourier transform, E =
View solution
Q. The distance of a synchronous satellite from Earth's surface is __________ km.
View solution
Q. A function having frequency f is to be sampled. The sampling time T should be
View solution
Q. Inverse Fourier transform of sgn (ω) is
View solution
Q. If I (s) = 5(s+250)/s(s+100) , the final value of i(t) is
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








