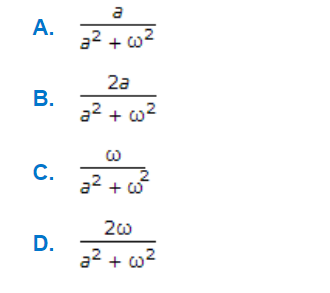
Q. Assertion (A): The wave shown in the given figure does not contain the dc component and even harmonics.

Reason (R): If f(- t) = f(t) the wave has only cosine terms.

View solution

Q. If £ f(t) = F(jω), then

View solution

Q. If n is the number of observations and r is the residue, the standard deviation σ =

View solution

Q. Consider these tow statements and answer follow:

View solution

Q. Consider following statements:

View solution

Q. Consider below given statements:

View solution

Q. The z transform of fk = a^k is

View solution

Q. In the given figure f(t) is an even function.

View solution

Q. Which of the following is not true for impulse function δ(t)?

View solution

Q. In the given figure the phase angle of Fn is either 0 or Π.

View solution

Q. For the function f(t) = e^(-at), the Laplace transform is

View solution

Q. The Z inverse of the given Z transform is

View solution

Q. Consider the following two statements :

View solution

Q. Consider the following two statements :

View solution

Q. If x(z) is the Z transform of sequence xk, the z transform of sequence (kxk)is

View solution

Q. If Sn is the power associated with each frequency component and S(f) is the sum of all these powers, normalised power spectral density is

View solution

Q. For the signal in the given figure the Fourier transform is 2sinωΤ₁, then the Fourier transform of the signal in the given figure

View solution

Q. Let x(t) ↔ X(jω) be F.T pair. The Fourier transform of the signal x(5t - 3) in terms of X(jω) is given as

View solution

Q. Assertion (A): The Fourier series of the wave shown in the figure does not contain even harmaonics.

Reason (R): If f(t) = - f(t ± T/2) the function is said to have half wave symmetry.

View solution

Q. The following table gives some time functions and the Laplace transforms. Of these correctly matched pairs are

View solution