Question
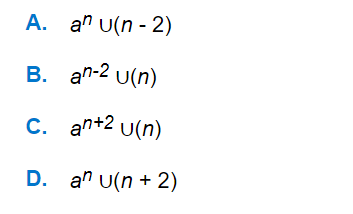
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. A discrete LTI system is non-casual if its impulse response is
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. If f(t) is an odd function
View solution
Q. The inverse z-transform of X(z) is
View solution
Q. The impulse response of the DT - LTI system is given below.
Check whether the system is
1. Stable
2. Casual
3.Dynamic
View solution
Q. For the single rectangular pulse of the given figure:
F(jω) = [Ad sin (ωd/2)]/(ωd/2).
View solution
Q. If p is the probability of success and q is the probability of failure, then the probability that there are r successes in n trails is
View solution
Q. A signal m(t) with bandwidth 500 Hz is first multiplied by a signal g(t) where g(t) ids given by below equation. The resulting signal is then passed through on ideal low pass filter with bandwidth 1 kHz. The output of the low pass filter would me
View solution
Q. The Z.T. of sequence x[n] = aⁿ ∪ [n] is
View solution
Q. The unit step response of a system is (1 - e^(at)) u(t). Then its impulse response is
View solution
Q. The inverse Laplace transform of 1/(s - a)² is
View solution
Q. Which one of the following digital filters does have a linear phase response?
View solution
Q. cos(nω1t) =
View solution
Q. Fourier transform of e^(-a|t|) is
View solution
Q. Assertion (A): The wave shown in the given figure does not contain the dc component and even harmonics.
Reason (R): If f(- t) = f(t) the wave has only cosine terms.
View solution
Q. If £ f(t) = F(jω), then
View solution
Q. If n is the number of observations and r is the residue, the standard deviation σ =
View solution
Q. Consider these tow statements and answer follow:
View solution
Q. Consider following statements:
View solution
Q. Consider below given statements:
View solution
Q. The z transform of fk = a^k is
View solution
Q. In the given figure f(t) is an even function.
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!