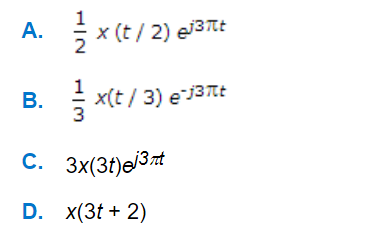
Q. An experiment is repeated N times. One event A occurs Nᴀ times. Then

View solution

Q. If f(t) is an even function, F(jω) =

View solution

Q. If Laplace transform of f(t) is F(s), then £[tf(t)] =

View solution

Q. The minimum sampling frequency in sample/sec. required to reconstruct the following signal from its samples without distortion would be

View solution

Q. The function shown in the given Figure can be written as

View solution

Q. In a network V(s) = Z(s) I(s) where V(s), Z(s) and I(s) are Laplace transforms of v(t), z(t) and i(t). The voltage v(t) is

View solution

Q. As per normal distribution the probability of an error between limits a and b is

View solution

Q. If F(jω) is the Fourier transform of f(t) then f(t) =

View solution

Q. The Laplace transform of sin ωt is

View solution

Q. If f(t) is an even function

View solution

Q. The waveform shown in the given Figure can be written as

View solution

Q. If a function f(t) is Laplace transformable, then

View solution

Q. In the given figure shows a periodic triangular wave. The Fourier series will have

View solution

Q. If x^k is one sided to the right

View solution

Q. A discrete LTI system is non-casual if its impulse response is

View solution

Q. If f(t) is an odd function

View solution

Q. The inverse z-transform of X(z) is

View solution

Q. The impulse response of the DT - LTI system is given below.
Check whether the system is

1. Stable
2. Casual
3.Dynamic

View solution

Q. For the single rectangular pulse of the given figure:
F(jω) = [Ad sin (ωd/2)]/(ωd/2).

View solution

Q. If p is the probability of success and q is the probability of failure, then the probability that there are r successes in n trails is

View solution