Question
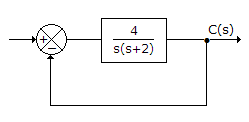
a.
s = 0 and s = -2
b.
s = 0, s = -1 ± j√3
c.
s = -1 ± j√3
d.
s = -2 and s = -1 ± j√3
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. For the system of the given figure the closed loop poles are located at
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The system in the given figure, x(0) = 0 and x (0) = 0, At t = 0 the unit impulse δ(t) is applied X(s)
View solution
Q. A second order system has damping ratio x and natural frequency ωn. The unit step response is
View solution
Q. The following response is
View solution
Q. For a first order system having transfer function 1/(1+sT), the unit step response is
View solution
Q. In the given figure, R2 >> R1. Then V₂(s)/V₁(s)
View solution
Q. For the system of the given figure, the closed loop poles are at
View solution
Q. In the given figure the input frequency f = 10(1/2 π RC)
View solution
Q. For the second order system given by following equation, damping ratio is
View solution
Q. In the given figure, P = 3 kg force. Then X(s) =
View solution
Q. The polar plot in the given figure is for the term
View solution
Q. The compensator in the given figure is a
View solution
Q. For the block diagram of the given figure, the equation describing system dynamics is
View solution
Q. For the given figure C(s)/R(s)
View solution
Q. The polar plot of
View solution
Q. For the system of the given figure, the undamped natural frequency of closed loop poles is
View solution
Q. In the given figure C(s)/U(s) =
View solution
Q. The signal flow graph of a system is shown in the given figure. The effect of disturbance TD can be reduced by
View solution
Q. A motor is coupled to a load through gear ratio n. If T is the motor torque, Jm and JL are moment of inertia of rotor and load, then torque to inertia ratio referred to motor shaft is
View solution
Q. In the given figure the input frequency f = 0.1 (1/2 π RC)
View solution
Q. The open loop frequency response of a unity feed back system is as given below. The gain margin and phase margin respectively are
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!