Question
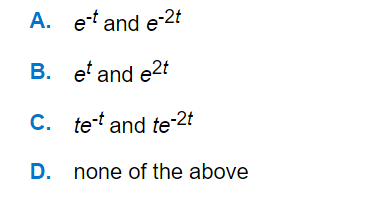
a.
A
b.
B
c.
C
d.
D
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. If F(s) = 2s+3 / (s+1)(s+2), the terms in f(t) will have
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. If F(s) is given by following equation, the coefficient of term e^(-t) in f(t) will be
View solution
Q. If f(t) = A d(t - a), F(s) is
View solution
Q. The sampling of a function f(l) = sin 2πf₀t starts from a zero crossing. The signal can be detected if sampling time T is
View solution
Q. If Laplace transform of f(t) is F(s), then £ f(t - a) u (t - a)= 0
View solution
Q. Assertion (A): The modified ramp function of the given figure can be represented s sum of two ramp functions of the given figure.
Reason (R): If f(t) = t, F(s) = 1
View solution
Q. Energy density spectrum of x[n] = aⁿ∪[n] for -1 < a < + 1 is
View solution
Q. Z transformer of
View solution
Q. Energy density spectrum of a gate GT(t) function is
View solution
Q. For the system in the given figure
View solution
Q. The Laplace transform of the waveform shown in the below figure is
View solution
Q. Laplace transform of e^(at) cos (at) is
View solution
Q. The value of the following equation in + ve sense is
View solution
Q. The amplitude of the first odd harmonic of the square wave shown in the given figure is
View solution
Q. The inverse Laplace transform of 1 / (s+1)³ is
View solution
Q. The final value of following is
View solution
Q. Let the Fourier transform of y(n) be given by below equation, then y(e^(j0)) is
View solution
Q. The value of following Integral is equal to
View solution
Q. The z transform of sequence x[n] = {2, 4, 3, 2}
View solution
Q. For the function u(t - a) = 0 for t < a and u(t - a) = 1 fort ≥ a, the Laplace transform is
View solution
Q. Consider the following statements :
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








