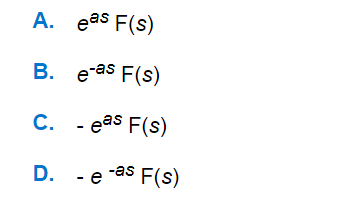
Q. Assertion (A): The modified ramp function of the given figure can be represented s sum of two ramp functions of the given figure.

Reason (R): If f(t) = t, F(s) = 1

View solution

Q. Energy density spectrum of x[n] = aⁿ∪[n] for -1 < a < + 1 is

View solution

Q. Z transformer of

View solution

Q. Energy density spectrum of a gate GT(t) function is

View solution

Q. For the system in the given figure

View solution

Q. The Laplace transform of the waveform shown in the below figure is

View solution

Q. Laplace transform of e^(at) cos (at) is

View solution

Q. The value of the following equation in + ve sense is

View solution

Q. The amplitude of the first odd harmonic of the square wave shown in the given figure is

View solution

Q. The inverse Laplace transform of 1 / (s+1)³ is

View solution

Q. The final value of following is

View solution

Q. Let the Fourier transform of y(n) be given by below equation, then y(e^(j0)) is

View solution

Q. The value of following Integral is equal to

View solution

Q. The z transform of sequence x[n] = {2, 4, 3, 2}

View solution

Q. For the function u(t - a) = 0 for t < a and u(t - a) = 1 fort ≥ a, the Laplace transform is

View solution

Q. Consider the following statements :

View solution

Q. The value of following Integral is equal to

View solution

Q. Consider the following two statements :

View solution

Q. A rectangular pulse train s(t) is shown in figure is convolved with the signal cos²(4π x 10³t). The convolved signal will be a

View solution

Q. The z-transform of sequence n x x[n] is

View solution