Question
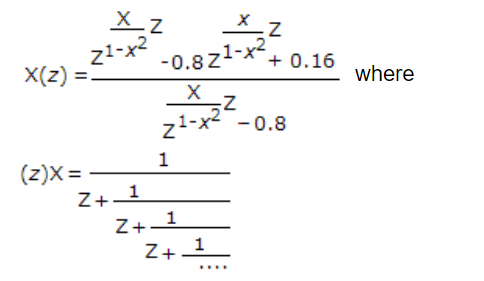
a.
casual and stable
b.
non-casual and stable
c.
non-casual and unstable
d.
casual and unstable
Posted under Electronics and Communication Engineering
Interact with the Community - Share Your Thoughts
Uncertain About the Answer? Seek Clarification Here.
Understand the Explanation? Include it Here.
Q. The z-transform of a particular signal is given below. The system after implementation will be
Similar Questions
Explore Relevant Multiple Choice Questions (MCQs)
Q. The system with given pole-zero diagram is
View solution
Q. A pole zero pattern of a certain filter is shown in figure. This filter must be
View solution
Q. The period of the following function is
View solution
Q. Let x(t) and y(t) with F.T. x(f) and y(f) respectively be related as shown in figure. Then y(f) is
View solution
Q. Laplace transform of a pulse function of magnitude E and duration from t = 0 to t = a is
View solution
Q. For the discrete time system of the given figure
View solution
Q. The final value theorem is
View solution
Q. If
View solution
Q. If F(s) = 2s+3 / (s+1)(s+2), the terms in f(t) will have
View solution
Q. If F(s) is given by following equation, the coefficient of term e^(-t) in f(t) will be
View solution
Q. If f(t) = A d(t - a), F(s) is
View solution
Q. The sampling of a function f(l) = sin 2πf₀t starts from a zero crossing. The signal can be detected if sampling time T is
View solution
Q. If Laplace transform of f(t) is F(s), then £ f(t - a) u (t - a)= 0
View solution
Q. Assertion (A): The modified ramp function of the given figure can be represented s sum of two ramp functions of the given figure.
Reason (R): If f(t) = t, F(s) = 1
View solution
Q. Energy density spectrum of x[n] = aⁿ∪[n] for -1 < a < + 1 is
View solution
Q. Z transformer of
View solution
Q. Energy density spectrum of a gate GT(t) function is
View solution
Q. For the system in the given figure
View solution
Q. The Laplace transform of the waveform shown in the below figure is
View solution
Q. Laplace transform of e^(at) cos (at) is
View solution
Recommended Subjects
Are you eager to expand your knowledge beyond Electronics and Communication Engineering? We've handpicked a range of related categories that you might find intriguing.
Click on the categories below to discover a wealth of MCQs and enrich your understanding of various subjects. Happy exploring!








